Python 3 データ分析試験　数式の基礎編

認定テキストは下記です。
1章から５章までありますが、今回は3章の数式の基礎の解説です。

Pythonによるあたらしいデータ分析の教科書 第2版

上記を読み込めば大丈夫なのですが
完全に読み込むのは初学者にはきついです。
そのため本記事では認定テキストを可能な限り要約してみました。

1.数式を読むための基礎知識

集合

集合の中身は{}を使って書くことができます。
A = {1,2,3,4}
B = {2,4,6,8}
∈は集合に入っていることを意味しています。
8は集合Bに入っていますので8∈Bと記述できます。
8は集合Aに入っていないので8∉

2つの集合の共通部分は積集合と呼ばれます。
A∩B = {2,4}と記述できます。
一方で全部を∪まとめたものは和集合と呼ばれます。
A∪B = {1,2,3,4,6,8}と記述できます。

数のまとまり
n個の数のまとまりを
\(x_1,\cdots,x_n\)
もしくは \(x_i(i=1,\cdots,n)\)
と表現します。

足し算の繰り返し
x₁からxₙまでをすべて足すという計算はシグマで表示できます。
\(\displaystyle \sum_{i=1}^{n}x_i\)

例えば　\(\displaystyle \sum_{i=1}^{10}i\)　の場合は1+2+3+4+5+6+7+8+9+10を意味します。

掛け算の繰り返し
x₁からxₙまでをすべてを掛け合わせるという計算はパイで表示できます。
\(\displaystyle \prod_{i=1}^{n} x_i\)

例えば　\(\displaystyle \prod_{i=1}^{10} i\)　の場合は1×2×3×4×5×6×7×8×9×10を意味します。

特殊な定数
円周率 \(\pi\) 程有名ではありませんがネイピア数 \(e\) があります。
\(e\) = 2.71828\(\cdots\)となっております。

\(n!\) は階乗と呼ばれ、nから順番に1まで掛け算をした値になります。
例えば\(6!\) の場合は6×5×4×3×2×1 = 720となります。
尚、\(0!\) = 1と定められています。

関数の書き方
関数は\(f\) や\(g\) など1文字で表現されることが多いです。
次の関数\(f\)は\(x\) を引数として受け取り、引数を2乗して1を足した値を返します。
\(f(x)=x^2+1\)

以下のように複数の引数をとる場合もあります。
\(f(x,y)=x^2-y^2+2\)

指数関数
\(f(x)=2^x\)の2の肩にある\(x\)を指数と呼びます。
以上のように関数の入力が別の数字の肩に乗って使われる関数を指数関数と呼びます。
この例では2を何乗するか？という意味です。
2は底と呼ばれ、底が1より大きな数字の時、\(x\)が大きくなると関数の値は大きくなっていきます。

指数関数を応用した関数にシグモイド関数があります。
機械学習のアルゴリズムであるニューラルネットワークでよく使われます。
\(f(x)=\displaystyle \frac{1}{1+e^{-x}}\)
\(x\)が大きくなると0に近付きますのでシグモイド関数の値は1に近付きます。
逆に\(x\)が非常に小さな値になると\(e^{-x}\)は大きな値になりシグモイド関数の値は0に近付きます。

対数関数
\(y=\log{_a} x\)のような数式で表現される関数を対数関数といいます。
例えば\(y=\log{_2} 8\)ならば2を3乗すれば8ですので答えは3となります。
例えば\(y=\log{_4} 16\)ならば4を2乗すれば16ですので答えは2となります。

底が10の時は常用対数と呼ばれます。
\(\log{_1}{_0}x\)と書きますが底の10が省略され\(\log{}x\)となることもあります。
同様に\(\log{_e} x\)も省略され\(\log{}x\)となることもあります。

0乗は1と定められています。
\(2^0\)、\(3^0\)、\(4^0\)もすべて1となります。
そのため対数関数\(f(x)\)の\(x\)が1の場合、つまり\(f(1)\)の解は0となります。

三角関数

5.線形代数学

ユークリッド距離の問題がありました。
ピタゴラス定理を活用して直線的な最短距離を算出する問題です。
c² = a² + b² 　っていう公式です。

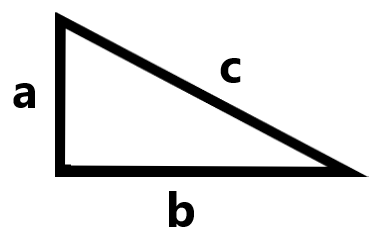
ピタゴラス定理は3次元、4次元となっても成立します
d² = a² + b² + c²
e² = a² + b² + c² + d²

行列の掛け算についてです。
m × s の行列にs × n の行列を掛けるとm × n の行列になります。

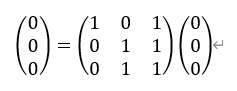
6.基礎解析

下記のような微分の問題が出題されておりました。
ネイピア数eのx乗を微分したらどうなるか？
答えは変化なしとなります。

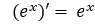
7.確率と統計

分散と標準偏差の定義は理解しておく必要があります。
データから平均値を引いた値を二乗します。
すべてのデータをそのようにしてデータ数で割った値が分散です。
その平方根が標準偏差となります。

相関係数についても理解しておきましょう。
相関係数はー1から1の間で変化します。
絶対値が1に近ければ相関が強く0に近ければ弱いといえます。

データの再代入についてです。
import numpy as np
a = np.array([1,2,3])
print(a)
a[2] = 4
print(a)

インデックス値[2]の値3を4に書き換えました。